Ibarat daun yang jatuh berguguran pada ranting pohon, jatuh sesuai massanya. Dari awal tumbuh daun itu berwarna hijau, akhirnya lama- lama daun itu pun semakin memudar, semakin menguning dan jatuh berguguran tinggalkan rantingnya. Tetapi, ranting yang ditinggalkan daun tadi tak mau lama- lama kosong tanpa daun yang mengisi. Akhirnya, tumbuhlah daun-daun baru yang jauh lebih menarik untuk dipandang karena kesegaran warnanya. Begitulah siklus itu terjadi terus menerus sampai ranting atau pohon tersebut patah bahkan mati. Ya, organisasi itu pun ibarat komponen pohon yang membuahkan ranting dan pada ranting- ranting itu pun melekat dedaunan yang akan memberi manfaat keteduhan bagi orang-orang yang bernaung di bawahnya.
Time flies so fast. Begitulah kata- kata yang mungkin hampir setiap insan katakan ketika amanah di suatu organisasi telah selesai. Pundak pun dirasanya lebih ringan.
Rasa seperti itu juga tentu dirasakan oleh pengurus Kabinet Optimal himpunan mahasiswa matematika 2016 yang kini telah bertransformasi dalam Kabinet Transformatif 2017. Memang bukanlah wajah- wajah asing yang mengisi himpunan kepengurusan tersebut, tapi kami yakin semangat mereka jauh lebih baru dan optimal dibanding kabinet sebelumnya. Memang idealnya seperti itu. Tidak mungkin sebuah ranting menumbuhkan daun yg layu, pasti yang ditumbuhkannya adalah daun yang lebih hijau dan segar dari sebelumnya.
Barakallahu wa innalillah untuk Rizky Anwari sebagai Ketua Himatika 2017 dan segenap himpunan pengurus Kabinet Transformatif 2017. Semoga bisa menjadi daun- daun segar yang meneduhkan orang-orang yang bernaung di bawahnya. Selamat bertransformasi sehingga idealitas- idealitas itu benar- benar menjadi sebuah realitas.
2016
Pemodelan matematika merupakan bidang matematika yang berusaha untuk mempresentasikan dan menjelaskan sistem-sistem fisik atau problem pada dunia real dalam pernyataan matematika sehingga diperoleh pemahaman dari problem dunia real ini menjadi lebih tepat. (Prayudi, 2006). Sederhananya, model matematika merupakan usaha untuk menggambarkan suatu fenomena ke dalam bentuk rumus matematis sehingga mudah untuk dipelajari dan dilakukan perhitungan.
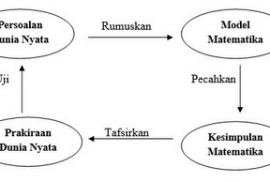
Tahapan Pemodelan Matematika
- Mengenali dan menamai variable bebas dan tak bebas serta membuat asumsi-asumsi seperlunya untuk menyederhanakan fenomena sehingga membuatnya dapat ditelusuri secara matematika.
- Menerapkan teori matematika yang telah diketahui pada model matematika yang telah dirumuskan guna mendapatkan kesimpulan matematikanya.
- Mengambil kesimpulan matematika tersebut dan menafsirkannya sebagai informasi yang berkaitan dengan permasalahan yang dimodelkan dengan cara memberikan penjelasan atau membuat perkiraan.
- Menguji perkiraan terhadap data riil. Jika perkiraan yang kita buat tidak sebading dengan kenyataan, maka model yang didapat perlu diperhalus atau merumuskan model baru dan memulai daur kembali. Bisa juga dengan memperbaiki asumsi-asumsi yang diberikan.
Jenis-jenis Model Matematika
Mahasiswa yang berkuliah di Program Studi S1 Matematika pasti akan dihadapkan dengan pilihan mata kuliah. Mata kuliah ini dikelompokkan dalam beberapa peminatan tertentu.
Kuliah di Matematika, sering kali kita mendengar orang- orang disekitar berkata, “Wah keren banget, kakak pintar yaaa” , “Hebat sekali”, dan sebagainya… Tapi pernahkan kita, sebagai lakon yang menjalani perkuliahan di Matematika, merasa jenuh? Well nyatanya cukup banyak mahasiswa matematika yang telah mengenyam pendidikan selama 1- 2 semester merasakan hal ini. Permasalahannya simpel…. materi matematika yang kita sukai di SMA ternyata hanya sebagian kecil dari mata kuliah di Jurusan Matematika, selebihnya? Selamat datang di dunia pembuktian!
Himpunan Mahasiswa Matematika UGM proudly present:
Seminar Nasional Matematika Ke-9
“Impementasi Logika Fuzzy untuk Mengatasi Permasalahan Bangsa”
oleh: Hana Safitri
Apa kabar mahasiswa? Sudah seberapa lamakah engkau menjadi mahasiswa? Kemungkina besar jawabnnya ada yang baru beberapa bulan saja, bahkan beberapa hari, ada yang sudah setahun bahkan bertahun-tahun. Bagaimana rasanya menjadi mahasiswa, mahasiswa baru? Apakah sesuai ekspektasi atau sebaliknya? Ada keluhan atau sudah bergelimang keluhan?
Yah, begitulah hidup. Setiap orang memiliki massanya masing-masing, ada massa di mana pundaknya semakin diberatkan dengan kewajiban-kewajiban yang kadang tak tahu dari mana asalnya. Terlebih lagi ketika seseorang memilih untuk meningkatkan levelnya, misal dari level anak SD menuju ke level SMP, tentu beban yang dipikulnya sudah tak seringan anak SD lagi, begitu juga ketika anak SMP memilih untuk menaiki levelnya menjadi anak SMA dan anak SMA yang memilih menaiki levelnya menjadi seorang mahasiswa atau yang lebih ekstrim lagi membina sebuah rumah tangga *woooow*. Di sini penulis menggunakan kata “memilih”, mengapa demikian? Karena untuk menaiki level itu tersendiri merupakan suatu pilihan, pilihan untuk menambah kewajiban-kewajiban yang ada pada tiap levelnya.
November ini salah satu dari program kerja terbesar Himatika mulai bergulir. Di naungi oleh departemen Apothema Himacup hadir sebagai ajang kompetisi antar angkatan. Dengan beberapa penyesuaian dari tahun sebelumnya, himacup tahun ini hadir bukan hanya berkompetisi event ini diharapkan mampu mempererat kekeluargaan antar angkatan di Himatika. Selain itu juga untuk wadah pencarian bakat guna persiapan menghadapi kompetisi yang lebih besar.
Beberapa perubahan di tahun ini meliputi pergantian cabang vocal solo menjadi akustik yang diharapkan mampu menambah antusias baik peserta maupun audiens yang hadir saat perlombaan. Selain itu ditambah dua cabang baru yaitu panco serta truft yang diharapkan juga mampu menambah ketat persaingan dalam kompetisi ini.
Hai semuanya! Bertemu lagi dengan artikel Lemma, yeayy *alay * abaikan.
Kali ini, kita akan membahas Logika Fuzzy. Apa itu?
Logika Fuzzy adalah peningkatan dari logika Boolean yang berhadapan dengan konsep kebenaran sebagian. Saat logika klasik menyatakan bahwa segala hal dapat diekspresikan dalam istilah biner (0 atau 1, hitam atau putih, ya atau tidak), logika fuzzy menggantikan kebenaran boolean dengan tingkat kebenaran.
Logika Fuzzy memungkinkan nilai keanggotaan antara 0 dan 1, tingkat keabuan dan juga hitam dan putih, dan dalam bentuk linguistik, konsep tidak pasti seperti “sedikit”, “lumayan”, dan “sangat”. Logika ini berhubungan dengan set fuzzy dan teori kemungkinan. Logika fuzzy diperkenalkan oleh Dr. Lotfi Zadeh dari Universitas California, Berkeley pada 1965.